≪接着・原賀塾≫
講師:(株)原賀接着技術コンサルタント
首席コンサルタント、工学博士
原賀康介

図7-13(再掲) 図7-2に変数の記号などを追加した図
① <Cv接着設計法>適用の前提 : <第5回>から<第7回>までで述べた高信頼性・高品質接着達成のための開発段階での作り込みの<目標値>の、初期の<凝集破壊率>は最低限40%以上確保されていて、<変動係数Cv>は0.10以下になるところまでは作り込まれていることを前提とします。
② 接着強度の分布の形 : 凝集破壊が前提なので<正規分布>で考えます。
③ 発生不良率 : 接着部に加わる最大の力Pmax以下のものが破壊すると考えます。
④ p : 耐用年数までに許容できる不良率の上限強度、言い換えると、良品の最低強度をpとします。
⑤ 要求信頼度 : 許容不良率F(x)または、工程能力指数の考え方を用いた信頼性指数 Rで表します。
許容不良率F(x)は1/100万などわかりやすいですが、式化しにくいので、工程能力指数の考え方を用いて、信頼性指数 Rを(6)式のように定義します。
信頼性指数R = (μ - p) / 3σ ・・・ (6)
μ:平均値 p:許容不良率の上限強度(良品の最低強度) σ:標準偏差
R は、1.33,1.50,1.67 が一般的。
⑥ ばらつきを表す指標 : 変動係数Cvとばらつき係数dを用います。
変動係数Cv = σ / μ σ:標準偏差 μ:平均値
・Cv値が小さいほどばらつきが小さい
・初期状態において最低限Cv≦0.10 が必要
ばらつき係数d = p / μ ・・・ (3)
= 1 - 3R・Cv ・・・ (7) 図7-9のグラフ
p : 許容不良率の上限強度(良品の最低強度) μ:平均強度
R:信頼性指数 Cv:変動係数
・dが1に近いほどばらつきが小さく分布がシャープで品質レベルが高い
⑦ 劣化による強度低下とばらつきの増大 :
耐用年数経過後の強度保持率 ηy = μy /μR0 ・・・(9)
μy:耐用年数経過後の平均値 μR0:初期の平均値
劣化後のばらつきの増大は、初期の変動係数が劣化後k倍に増大すると考えます。
劣化後の変動係数 Cvy = k ・CvR0 ・・・(10)
k:劣化による変動係数の増加率 CvR0:初期の変動係数
1.0 ≦ k ≦ 1.5(講師の経験値)
⑧ 温度係数 :
温度係数 ηT = μT / μR0 ・・・(11)
μT :接着強度が最も低くなる温度での平均強度 μR0:室温での平均強度
⑨ 内部破壊係数 :
内部破壊係数h = 内部破壊発生開始強度 / 破断強度 ・・・(12)
1) 静的荷重負荷のみの場合:h1 = 0.50
2) 高サイクル繰返し負荷の場合:h2 = 0.25
3) 低サイクル繰返し負荷の場合:h3 = 0.4~0.5
⑩ 安全率 :
安全率 S = 設計基準強度 / 設計許容強度
安全率 S = 1.5 ~(2.0)
⑪ <設計許容強度>と<接着部に加わる最大力>の関係 :
設計許容強度pW ≧ 接着部に加わる最大力Pmax ・・・(13)
7.6 必要な<初期室温平均値μR0>の算出式
結論を先に示します。必要な<初期室温での平均強度μR0>は、 (14)式、 (15)式で計算します。
(1)初期室温でのばらつき係数dR0を設定して求める場合
μR0 ≧ Pmax ・S /〔ηy {1 - k・ (1 - dR0) } ・ηT・h 〕 ・・・ (14)
(2)信頼性指数Rと初期室温での変動係数CvR0を設定して求める場合
μR0 ≧ Pmax・S / {ηy (1 - k・3R・CvR0)・ηT・h } ・・・ (15)
Pmax : 接着部に加わる最大力
S : 安全率 7.5の⑩参照
ηy : 耐用年数経過後の強度保持率 7.5の⑦参照
k : 劣化による変動係数の増加率 7.5の⑦参照
dR0 : 初期室温でのばらつき係数 7.5の⑥参照
R : 信頼性指数 7.5の⑤参照
CvR0: 初期室温での変動係数 7.5の⑥参照
ηT : 温度係数 7.5の⑧参照
h : 内部破壊係数 7.5の⑨参照
(1)の場合、必要な<初期室温でのCv値>CvR0は、 (8)式から算出できます。ただし、あらかじめ、<信頼性指数R>が規定されていることが必要です。
CvR0=(1-d R0)/3R ・・・(8)
R=1.67 の場合、CvR0=(1-dR0)/5.0
R=1.50 の場合、CvR0=(1-dR0)/4.5
R=1.33 の場合、CvR0=(1-dR0)/4.0
R=1.00 の場合、CvR0=(1-dR0)/3.0
(2)の場合、<初期室温でのばらつき係数>dR0は、(7)式から算出できます。
dR0 = 1 - 3R・Cv R0 ・・・ (7)
なお、 (14)式の k ・ (1 - dR0) 、 (15)式の k・3R・CvR0 は、1より小さくなければなりません。
7.7 【補足】 (14)式、 (15)式の求め方
まず、劣化後の想定不良率の上限強度pyを求めます。
劣化後のばらつき係数dy = py / μy 、
劣化後の平均強度μy = μR0・ηy 、なので、
劣化後のばらつき係数dy = py / (μR0・ηy) となり、
また、 (7)式より、dy =1- 3R・Cvy、 (10)式より、Cvy=k・CvR0 なので、
劣化後のばらつき係数dy = 1 - 3R・k・CvR0 となります。
よって、py / (μR0・ηy) =1 - 3R・k・CvR0 となるので、劣化後の想定不良率の上限強度py は、 (16)式となります。
py = μR0・ηy (1 - k・3R・CvR0) ・・・ (16)
CvR0=(1-d R0)/3R ・・・(8)なので、 (16)式のCvR0を置き換えると(17)式となります。
py = μR0・ηy〔1 - k・(1-d R0)} ・・・ (17)
次に、 (16)式、 (17)式に温度係数ηT 、内部破壊係数hを掛け合わせ、さらに安全率Sで割ると、(16’)式、 (17’)式となり、<設計許容強度>pW が求まります。
設計許容強度pW = μR0・ηy (1 - k・3R・CvR0)・ηT・h / S1 ・・・ (16‘)
設計許容強度pW = μR0・ηy〔1 - k・(1-d R0 )} ・ηT・h / S1 ・・・ (17‘)
最後に、設計許容強度pW ≧ 接着部に加わる最大力Pmax ・・・(13) なので、
Pmax ≦ pW = μR0・ηy (1 - k・3R・CvR0)・ηT・h / S1 ・・・ (16”)
Pmax ≦ pW = μR0・ηy〔1 - k・(1-d R0 )} ・ηT・h / S1 ・・・ (17”) となり、 (14)式、 (15)式が得られます。
7.8 計算例
要求されている条件(設定値)として、
① 接着部に加わる最大力Pmax は200N
② 信頼性指数Rは1.50を確保すること
③ 初期室温でのばらつき係数d R0は0.70以上あること
があり、その他の変数を以下と仮定します。
④ 劣化後の強度保持率ηy は 0.7
⑤ 劣化による変動係数の増加率k は 1.2
⑥ 温度係数ηT は 0.7
⑦ 内部破壊係数h は 0.5
⑧ 安全率S は 1.5
これらの数字を(14)式に当てはめると、
μR0 ≧ Pmax・ S /〔ηy {1 - k・ (1 - dR0 ) }・ηT・h 〕 ・・・ (14)
≧ 200×1.5 /〔0.7× {1 - 1.2 × (1 - 0.70)} × 0.7×0.5 〕
≧ 1,913(N)
となり、初期の室温平均強度μR0 は、接着部に加わる最大力Pmaxの9.6倍以上必要なことがわかります。
例えば、初期室温でのせん断接着強さτが20MPaの接着剤を用いて、接着面積全体に均一に力が加わると仮定すると、必要な接着面積は、1,913N/20MPa=96mm2となります。(例えば10mm×10mm)
また、初期に必要な変動係数CvR0は、 (8)式より、
CvR0 =(1-d R0)/3R ・・・(8)
=(1-0.70)/(3×1.50)
=0.067
と算出されます。
これらの結果から、接着面積の点からは適用できる可能性は高いが、変動係数0.067以下で安定して生産するには相当な努力が必要で、実質的に困難と言うことも考えられます。こういう場合は、変動係数0.10で生産するとどうなるのかと言うことを知りたくなります。
こういう場合は、(15)式で、初期の変動係数CvR0を0.10として計算してみます。
μR0 ≧ Pmax・S / {ηy (1 - k・3R・CvR0)・ηT・h } ・・・ (15)
≧ 200・1.5 / {0.7 × (1 - 1.2×3×1.50×0.10)×0.7×0.5}
≧ 2,662(N)
となり、初期の室温平均強度μR0 は、接着部に加わる最大力Pmaxの13.3倍以上必要なことがわかります。初期室温でのせん断接着強さτが20MPaの接着剤を用いると仮定すると、必要な接着面積は、2,662N/20MPa=133mm2となります。(例えば10mm×13mm)
少し接着面積を大きくして平均強度を上げることで楽に生産できることがわかります。
ただし、初期室温でのばらつき係数を計算してみると、
ばらつき係数d = 1 - 3R・Cv ・・・ (7) なので、
dR0 = 1 - 3R・Cv R0 = 1-3×1.50×0.10 = 0.55 となり、上記の要求条件③「初期室温でのばらつき係数d R0は0.70以上あること」を満足できないことがわかります。しかし、初期の許容不良率の上限強度、即ち、良品の下限強度pR0を、 (3)式で計算してみると、
ばらつき係数d = p / μ ・・・ (3) なので、
pR0 = dR0・μR0 = 0.55×2,662 = 1,464(N) となります。
(14)式で算出した初期に必要な室温平均強度μR0は1,913Nで、ばらつき係数の要求値は0.70なので、良品の下限強度pR0は、(3)式から、pR0 = dR0・μR0 = 0.70×1,913 = 1,339 (N) となります。要求条件を満足できないにしても、良品の下限強度pR0はむしろ高くなっています。
変動係数Cv、信頼性指数R、ばらつき係数dは、 (7)式 や 図7-9で示したように、相互に関係しているので、製造のしやすさ(Cv)、信頼性(R)、品質(d)の観点から、最適条件を探る必要があります。
変数の数値を変えて種々の条件で計算してみると、接着部に加わる最大力Pmaxに対する初期室温平均強度μR0 の倍率は、10倍から50倍程度となる場合が多く見られます。
余談ですが、私が若い頃から、ものづくりに接着を活用している技術者の方々と雑談をしていると、「接着の安全率はどのくらい取れば良いのか」という話になり、「経験的に30倍から40倍程度かな」というところに落ち着くことが多々ありました。Cv接着設計法では、従来から使われてきた「安全率」という中身を、ばらつき、劣化、温度、内部破壊、その他の安全率などに分解して考えてきたので、安全率は1.5倍程度としましたが、接着部に加わる最大力の10倍から50倍程度という計算結果とほぼ合致しています。実際に設計や製造に携わってきた技術者たちの設定は妥当だったと言うことが言えるようです。
7.9 (参考)界面破壊で変動係数が大きい場合の計算例
<Cv接着設計法>を使用する場合の前提としては、7.5①に記したように、「高信頼性・高品質接着達成のための開発段階での作り込みの<目標値>の、初期の<凝集破壊率>は最低限40%以上確保されていて、<変動係数Cv>は0.10以下になるところまでは作り込まれていること」としています。
上記の前提からは外れますが、界面破壊で変動係数が大きい場合は、接着部に加わる最大力Pmaxに対して、初期室温での平均強度μR0はどのくらいになるのかを計算してみます。条件としては、7.8の条件を基本としますが、界面破壊で初期の変動係数が大きいという点から各係数の数字は以下のように変えています。
① 接着部に加わる最大力Pmax は200N ← 変更なし
② 信頼性指数Rは1.50を確保すること
← 1.00に変更します
※1.33以上ではエラーとなるため
③ 初期室温でのばらつき係数d R0は0.70以上あること
← 今回は(15)式を用いるので変動係数CvR0を設定します
← 初期の変動係数CvR0=0.16とします
※0.20としたいところですが、0.17以上ではエラーとなるため
④ 劣化後の強度保持率ηy は 0.7
← 0.4に変更します
※界面破壊では凝集破壊より劣化が大きくなるため
⑤ 劣化による変動係数の増加率k は 1.2
← 2.0に変更します
※2.0倍以上になる場合も多いですが、2.0倍より大きくするとエラーとなるため
⑥ 温度係数ηT は 0.7
← 0.5に変更します
※界面破壊では凝集破壊より強度低下が大きくなるため
⑦ 内部破壊係数h が 0.5
← 0.1に変更します
※界面破壊では大きく低下するため。<第6回>の6.1(5)参照下さい
⑧ 安全率S1 が 1.5
← 2.0に変更します
※もっと大きくしたいですが、2.0より大きい倍率ではエラーとなるため
上記の「エラーとなる」のは、7.6で述べた、 (14)式の k・ (1 - dR0) 、 (15)式の k・3R・CvR0 が、1以上となってしまうということです。
①~⑧の数値を(15)式に入れて計算すると、初期室温で必要な平均強度μR0は500,000Nとなり、接着部に加わる最大力Pmaxのなんと2,500倍もの強度が必要となります。せん断強度が20MPaの接着剤を使用すると仮定すると、25,000mm2(158mm角)もの接着面積が必要となります。なお、良品の最低強度(許容不良率の最大強度)pR0は平均値の52%の260,000Nが確保できます。
この結果から、界面破壊で初期の変動係数が大きいと、そもそも高い信頼性が確保できず(信頼性指数Rは1.00以下しか確保できない)、非常に大きな接着面積が必要となり、接着を採用するのは困難な状態になることがわかると思います。凝集破壊で変動係数を小さくすることが、高信頼性・高品質接着にとって、いかに重要かがおわかりいただけるでしょう。
7.10 <Cv接着設計法>のExcel計算シート
(14)式 や (15)式 を用いて計算することは簡単ですが、変数が多いので煩わしさを感じます。そこで、数字を入力するだけで結果が得られる表7-1に示す計算シート<Cv接着設計法計算シート>を作っています。下記からダウンロードできるので、活用して下さい。
表7-1 Cv接着設計法計算シート

7.11 最後に考えること
(1)必要な接着強度と部品自体の強度の関係
<Cv接着設計法>で<初期室温での必要な平均接着強度μR0>を見積もると、接着部の強度が接着される部品の強度を超えてしまう結果となることもあります。この場合、部品の材料を厚くしたり強度の強い材料に変更したりしなければならないとは考えないで下さい。製品の状態では、部品には、<接着部に加わる最大力Pmax>までの力しかかかりません。部品の強度は、耐用年数まで問題なく耐えられる強度があれば、接着部の強度以下でも問題はありません。
ただ、実際に接着部の強度を測定する場合は、接着部が壊れる前に部品が壊れてしまい、評価試験ができなくなってしまいます。評価試験のためには、部品の厚さを厚くしたり、より高強度な材料を用いたりする工夫が必要となります。
(2)接着部の構造設計
<第8回>の7.1<Cv接着設計法>とは で、<Cv接着設計法>は、「評価試験などを行っていない開発初期の段階で、初期(劣化前)室温での接着部の必要平均強度と必要変動係数Cv値を簡易に見積もる方法」と述べました。また、図7-1には、「接着部の構造や接着部内の応力値などは今は考えない」と書きました。
<Cv接着設計法>で必要強度の見積りができたら、次は、接着部の詳細設計に移ります。
接着部の構造は、部品の構造によって大きく異なりますが、接着部の大まかな構造のイメージはお持ちでしょう。
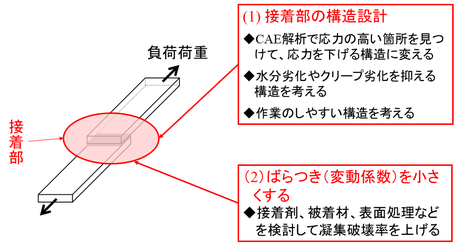
図7-14 必要な強度と変動係数の見積もり後に行うこと
接着部全体が均一に力を分担すれば良いのですが、接着部の構造や接着剤の物性、力が加わる速度などによっては、接着部の一部に大きな力が加わる、いわゆる<応力集中>が生じます。接着部の破壊は応力が高い箇所から生じやすく、応力が高い部分では劣化も起こりやすくなります。ですから、応力が高い部分を見つけ出して、応力を下げる工夫が必要となります。応力の高い箇所を見つけるには、有限要素法(FEM)解析を行うのが良いでしょう。解析の精度は問いません。接着部の応力が高い場所を見つけて、構造を変えて応力値が低くなる構造を見つければそれで十分です。
また、水分劣化やクリープ劣化は、接着の耐久性に大きな影響を及ぼす要因ですが、構造的に劣化を抑えることが可能です。詳細は別の機会に「耐久性」のところで述べることにします。
なお、接着部の構造は、接着作業のしやすさに直結しています。作業がやりやすい構造は、ばらつきを減らして品質を向上させることに繋がります。作業のしやすい構造を考えて下さい。
(3)凝集破壊率の向上
凝集破壊率を高くして変動係数Cvを小さくすることは、<初期室温で必要な平均強度μR0>を低下させる、即ち、接着面積を小さくして部品の小型化やコストダウンを図ることに繋がります。凝集破壊率を向上させる方法についても、別の機会に述べますが、接着剤、部品の材質・表面状態、接着部の構造、接着層の厚さ、内部応力などが影響するので、それらを最適化する検討が必要です。
<第7回>の6.高信頼性・高品質接着達成のための開発段階での作り込みの<目標値>の6.3必要強度 の求め方として、<第8回>から3回にわたって、<Cv接着設計法>について述べてきました。ここまでで、凝集破壊率、変動係数、接着強度の目標は見えてきたと思います。次の段階は、どうやって目標を達成するかです。次回から種々述べていきますが、次回は、6.2(7)でお約束していたばらつきの少ない引張せん断試験片の作製方法について説明します。
|
【PR】コンサル業務を受け付けています 弊社では、企業での開発や不具合対策の支援や社員向け教育などの業務を行っています。 課題を有しておらる場合は、お気軽にお問い合わせ下さい。
詳細はこちらをご覧ください。 |
| <接着・原賀塾>の掲載内容は、著作権法によって保護されており、著作権は原賀康介に帰属します。引用、転載などの際は弊社までご連絡ください。(会社内や団体・学術機関・研究機関内でのご活用に関してはこの限りではありません。) |
-------------------------------------------------------------------------------------

株式会社 原賀接着技術コンサルタント
